Beam parameter product

In laser science, the beam parameter product (BPP) is the product of a laser beam's divergence angle (half-angle) and the radius of the beam at its narrowest point (the beam waist).^[1] The BPP quantifies the quality of a laser beam, and how well it can be focused to a small spot.

A Gaussian beam has the lowest possible BPP, 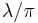$\lambda/\pi$ , where $\lambda$ is the wavelength of the light.^[1] The ratio of the BPP of an actual beam to that of an ideal Gaussian beam at the same wavelength is denoted M² ("M squared"). This parameter is a wavelength-independent measure of beam quality.

There are several ways to define the width of a beam. When measuring the beam parameter product and M², one uses the D4σ or "second moment" width of the beam to determine both the radius of the beam's waist and the divergence in the far field. Other definitions of beam quality have been used in the past, but the one using second moment widths is most commonly accepted.^[2]

The quality of a beam is important for many applications. In fiber-optic communications beams with an M² close to 1 are required for coupling to single-mode optical fiber. Laser machine shops care a lot about the M² parameter of their lasers because the beams will focus to an area that is M² times larger than that of a Gaussian beam with the same wavelength and D4σ waist width; in other words, the fluence scales as 1/M². The general rule of thumb is that M² increases as the laser power increases. It is difficult to obtain excellent beam quality and high average power (100 W to kWs) due to thermal lensing in the laser gain medium.

Measurement of the BPP

The BPP can be easily measured by placing an array detector or scanning-slit profiler at multiple positions within the beam after focussing it with a lens of high optical quality and known focal length. To properly obtain the BPP and M² the following steps must be followed:^[3]

Measure the D4σ widths at 5 axial positions near the beam waist (the location where the beam is narrowest).
Measure the D4σ widths at 5 axial positions at least one Rayleigh length away from the waist.
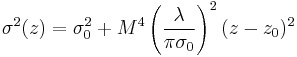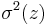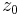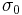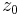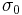Fit the 10 measured data points to $\sigma^2(z) = \sigma_0^2 %2B M^4 \left(\frac{\lambda}{\pi\sigma_0}\right)^2(z-z_0)^2$ ,^[4] where $\sigma^2(z)$ is the second moment of the distribution in the x or y direction (see section on D4σ beam width), and $z_0$ is the location of the beam waist with second moment width of $\sigma_0$ . Fitting the 10 data points yields M², $z_0$ , and $\sigma_0$ . Siegman showed that all beam profiles — Gaussian, flat top, TEMxy, or any shape — must follow the equation above provided that the beam radius uses the D4σ definition of the beam width. Using other definitions of beam width does not work.

In principle, one could use a single measurement at the waist to obtain the waist diameter, a single measurement in the far field to obtain the divergence, and then use these to calculate the BPP. The procedure above gives a more accurate result in practice, however.

References

^ ^a ^b "Beam parameter product". Encyclopedia of Laser Physics and Technology. http://www.rp-photonics.com/beam_parameter_product.html. Retrieved 2006-09-22.
^ A. E. Siegman, "How to (Maybe) Measure Laser Beam Quality," Tutorial presentation at the Optical Society of America Annual Meeting, Long Beach, California, October 1997.
^ ISO 11146-1:2005(E), "Lasers and laser-related equipment — Test methods for laser beam widths, divergence angles and beam propagation ratios — Part 1: Stigmatic and simple astigmatic beams."
^ A. E. Siegman, "How to (Maybe) Measure Laser Beam Quality," Tutorial presentation at the Optical Society of America Annual Meeting Long Beach, California, October 1997, p.9. (Note that there is a typo in equation on page 3. Correct form comes from equations on page 9.)